【よくわかる】量子力学とは何か?粒子性と波動性・測定時の不確定関係
はじめに
素粒子・原子・分子などの量子は、粒子性と波動性を合わせ持ち、測定時に不確定関係を示します。
意味が分からないと思うので、以下、説明します。
量子力学の意味
辞書には、「素粒子・原子・分子などの微視的な系を記述する力学体系。シュレーディンガー方程式にしたがう状態を導入、観測によって得られる測定値との間に確率的な解釈を行うことで、量子がもつ波動と粒子の二重性、測定における不確定関係などを矛盾なく説明する。量子力学は粒子および粒子集団を扱う現代物理学の基礎理論として、一方では原子核論・物性論へ、また一方で素粒子論・場の理論へと進展した」とあります。
つまり、「素粒子などの量子は、波動と粒子の性質を合わせ持ち、測定すると不確定な結果になる」ということです。
多分、何を勉強しても、釈然としないと思います。
それは、まだ未知の部分があるからだと思います。
以下、量子力学についてまとめます。
量子力学のまとめ
物理方程式
ニュートンの運動方程式「ma=F」があります。
「m」は物体の質量で、「a」は加速度、「F」は外力で、物体mに外力Fが作用して運動する時、加速度aに比例するという式です。
この式は、長らく物の運動の説明に重宝されましたが、1900年に、これでは説明つかない物体が、発見されたのです。
それが、量子です。
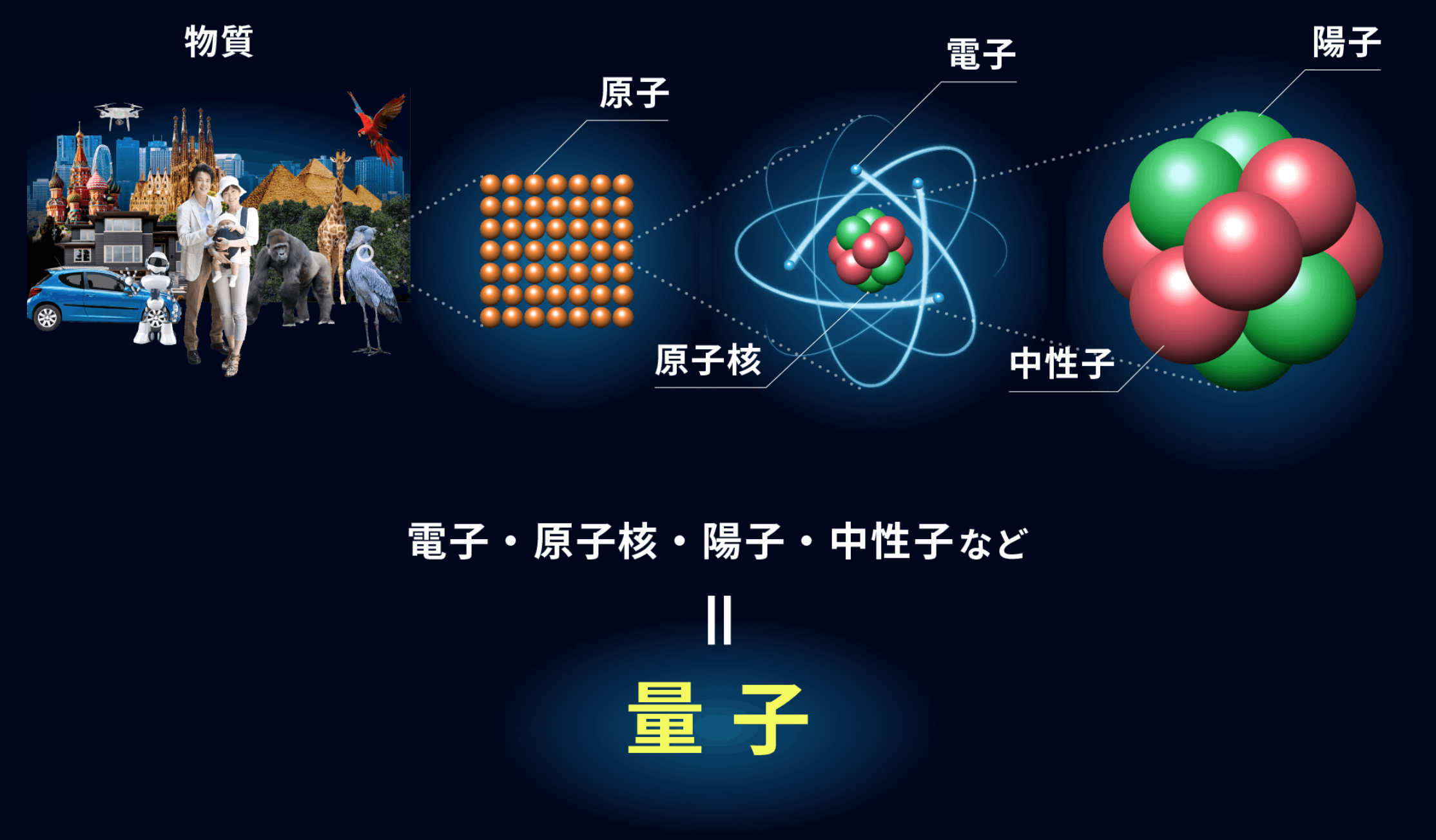
出典:日本経済新聞
原子の世界では、ニュートンの運動方程式が、成り立たなかったのです。
波動と粒子の性質を合わせ持つ
物理学には、「粒子性」と「波動性」という2つの概念があります。
粒子性では、ニュートンの運動方程式が成立します。
一方、波動性では、波動方程式を用います。
ここで、「光は、粒子なのか波なのか」という論争が起こりました。
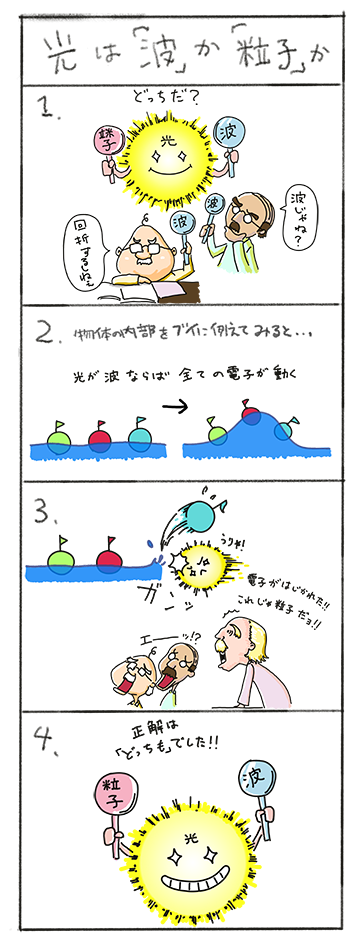
はじめは、「回折現象」が起きるため、波だという主張が優勢でした。
回折現象とは、「波動の伝播が障害物で一部さえぎられたとき、障害物の影の部分にも波動が伝播してゆく現象。障害物の大きさと波長が同程度のとき顕著になる。音波・電磁波・光・ X 線のほか、電子線・中性子線などの粒子線でも、その量子力学的な波動性のために回折が起こる」という意味です。
ところが、「光電効果」という現象が発見されて、論争に火がつきました。
光電効果とは、「物質に光を当てた時、物質内の電子が光子のエネルギーを吸収して起こる現象。電子が物質外に放出される外部光電効果と、物質内部で電子が移動して電流が流れたり、起電力を生じたりする内部光電効果とがある」という意味です。
上図を参考に、海に浮かぶブイを思い浮かべてください。波が来ると、全てのブイが、連関して動きます。一方、連関していなければ、ブイは、一つだけ動きます。物体は、たくさんの電子が集まってできています。だから、光が波ならば、光をぶつけると、全ての電子が連関して動くはずです。ところが、光を当てた物体から、電子が、一つだけ飛び出したのです。
この結果から、光は、粒子と波動の2つの性質を合わせ持つということが分かりました。
そんな粒子を「量子」と名付けたのです。
そして、この量子のために、「シュレディンガー方程式」が、導き出されたのです。
シュレディンガー方程式とは、「量子力学で、物質波を表す波動関数の時間的変化を決める微分方程式。系の全エネルギーに対応する演算子ハミルトニアンによる波動関数の変化が、波動関数の時間的変化に相応しているという形式で示される」という意味です。
相対性理論
アインシュタインは、3次元の世界に「時間」を加えて、「相対性理論」を発案しました。
つまり、3次元で考えていた理論は、時間が異なると、別の結果を招くのです。
量子力学では、相対性理論と量子力学を合わせた「相対論的量子力学」を使います。
さらに、シュレディンガー方程式に相対性理論を組み合わせた「ディラック方程式」というのも発案されています。
公式
粒子性と波動性に関する公式です。
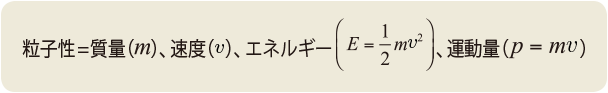
粒子が伴う性質は、質量や速度、エネルギー、運動量です。運動量は、「どのくらい重い物が、どのくらいの速度で動いているか」を示します。

波の伴う性質は、波の山がいくつあるのかという波数ベクトルや周波数です。波動方程式を解くと出てくるのが、平面波の式です。

粒子性と波動性との関係は、アインシュタインード・ブロイ関係式で表せます。
粒子性と波動性に関する動画
この動画の実験でも分かるように、測定をしないで実験をすると波動の結果を示し、測定をすると粒子の結果を示すのです。
これが、測定における不確定関係というものです。
量子もつれ
量子もつれは、一方の量子が答えを出すと、どんなに離れていても、他方の量子も他方の答えを出す現象です。
未知のこと
結局、量子がなぜ粒子性と波動性の性質を合わせ持つかは、未知のようです。
結論
量子は、様々な条件によって、粒子のように振る舞うこともあるし、波のように振る舞うこともあります。そこで、観測されるまでは、波のように振る舞っていると考えます。
参考サイト
姉妹サイト
量子コンピュータとは 量子コンピュータの仕組み・原理とは 量子力学とは 量子ビットチップ素子の構造 量子コンピュータの種類・分類・方式 量子コンピュータの歴史・年表・変遷 量子コンピュータの性能比較 量子コンピュータのメリット/デメリット スーパーコンピュータとの違い 量子コンピュータの活用事例 暗号解読のできる量子コンピュータ 量子コンピュータ関連銘柄 サブスクリプション免責事項・著作権表示
情報が古かったり、間違っていることなどによる損害の責任は負いかねますので、ご了承ください。
Copyright (C) SUZ45. All Rights Reserved.